فرمول های ریاضی
یک ضلع × خودش = مساحت مربع
یک ضلع × 4 = محیط مربع
طول × عرض = مساحت مستطیل
2× (طول + عرض) = محیط مستطیل
2 ÷ (قاعده × ارتفاع) = مساحت مثلث
مجموع سه ضلع = محیط مثلث
نصف ارتفاع × (قاعده بزرگ + قاعده کوچک) = مساحت ذوزنقه
مجموع 4 ضلع = محیط ذوزنقه
2÷ (قطر بزرگ × قطر کوچک) = مساحت لوزی
یک ضلع × 4 = محیط لوزی
ارتفاع × قاعده = مساحت متوازی الاضلاع
مجموع دو ضلع متوالی × 2 = محیط متوازی الاضلاع
عدد پی × مجذور شعاع = مساحت دایره
14/3 × شعاع × شعاع
14/3 × قطر = محیط دایره
مساحت کره
چهار ×عدد پی × مجذور شعاع = مساحت کره
حجم کره
عدد پی × شعاع به توان 3 = حجم کره
14/3 × (نصف قطر کوچک × نصف قطر بزرگ) = مساحت بیضی
یک ضلع × تعداد اضلاع = محیط چند ضلعی منتظم
طول یال × مساحت یک وجه = حجم مکعب
ارتفاع × عرض × طول = حجم مکعب مستطیل
ارتفاع × قاعده = حجم مکعب
ارتفاع هرم × مساحت قاعده هرم = حجم هرم
ارتفاع × مساحت قاعده = حجم استوانه
ارتفاع × محیط قاعده = مساحت جانبی
سطح دو قاعده + مساحت جانبی = سطح کل استوانه
مجموع مساحت سطوح جانبی = مساحت جانبی منشور
مجموع مساحت دو قاعده + مجموع مساحت سطوح جانبی = مساحت کلی منشور
ارتفاع × مساحت قاعده = حجم مخروط
تعاریف هندسی
شعاع : خطی از مرکز دایره به پیرامون دایره را شعاع می گویند.
(شعاع خطی مستقیم است که مرکز دایره را به نقطه ای از محیط دایره وصل می کند)
شعاع نصف قطر است.
قطر : فاصله مستقیم دو طرف دایره را که از وسط دایره بگذرد را قطر می نامند.
عدد پی : 14/3 = π یکی از معروف ترین ثابت های ریاضی عدد π می باشد.
عدد پی نسبت محیط دایره به قطرش است و تقریبا برابر 14/3 می باشد.
و دقیقتر آن 14159/3
و دقیقتر آن تا 22 رقم اعشاری برابر است با :
1415926535897932384626/3 = π
عدد پی (π) عددی گنگ است که رقم هایش تا بی نهایت ادامه دارد.
*برای بدست آوردن مساحت و محیط دایره، کره و بیضی از عدد ثابت پی استفاده می شود.
زاویه حاده (زاویه تند) : زاویه کوچکتر از 900 را حاده یا تند گویند.
زاویه قائمه : برابر 900 می باشد.
زاویه منفرجه (زاویه باز) : زاویه بیشتر از 900 را زاویه باز یا منفرجه نامند.
زاویه نیم صفحه : زاویه 1800 را زاویه نیم صفحه گویند. همانند نیم دایره
درجه = واحد اندازه گیری زاویه، درجه است.
حداکثر زاویه (تمام صفحه) 360 درجه است. همانند دایره
نیم ساز : نیم خطی که زاویه را به دو قسمت مساوی تقسیم می کند را نیمساز زاویه گویند.
دو خط عمود بر هم : دو خط که زاویه بین آنها راست یا 900 باشد دو خط عمود بر هم هستند.
عمود منصف : عمود منصف خطی است که هم عمود بر پاره خط بوده و هم آن را نصف کرده باشد.
خط تقارن = اگر شکلی را از وسط تا کنیم طوری که تمامی زوایای آن شکل بر هم منطبق شوند، محل تا شدگی را خط تقارن نامند.
بخش پذیری اعداد
حاصل تقسیم صفر بر هر عددی برابر صفر است.
حاصل تقسیم هر عددی بر صفر تعریف نشده است. یا می توان گفت بی نهایت است.
اعدادی بر 2 قابل تقسیم هستند که یکان آنها زوج باشد.
اعدادی بر 3 قابل تقسیم هستند که مجموعشان بر 3 قابل تقسیم باشد.
اعدادی بر 4 قابل تقسیم هستند که دو رقم آخر آنها بر 4 قابل تقسیم باشد.
هر عددی که مضربی از 100 باشد نیز بر 4 قابل تقسیم است. (چون 100 خودش بر 4 قابل تقسیم است.)
اعدادی بر 5 قابل تقسیم هستند که رقم یکان آنها 0 یا 5 باشد.
اعدادی بر 6 قابل تقسیم هستند که بر 2 و 3 قابل تقسیم باشند.
عددی بر 8 قابل تقسیم است که یا مضربی از 1000 باشد و یا 3 رقم آخر آن بر 8 قابل تقسیم باشد.
اعدادی بر 9 قابل تقسیم هستند که مجموعشان بر 9 قابل تقسیم باشد.
عددی بر 10 قابل تقسیم است که رقم آخر آن صفر باشد.
عددی بر 11 قابل تقسیم است که اگر ارقام آن عدد را به ترتیب از چپ به راست یکی در میان منها و جمع کنیم، حاصل صفر یا مضربی از 11 باشد.
اعدادی بر 12 قابل تقسیم هستند که بر 3 و 4 قابل تقسیم باشند.
اعدادی بر 14 قابل تقسیم هستند که بر 7 و 2 قابل تقسیم باشند.
اعدادی بر 15 قابل تقسیم هستند که بر 3 و 5 قابل تقسیم باشند.
هر تقسیم از چهار قسمت تشکیل شده است :
مقسوم، مقسوم علیه، خارج قسمت، باقیمانده.
باقیمانده + مقسوم علیه × خارج قسمت = مقسوم
اعداد
اعداد طبیعی :
اعداد صحیح بزرگتر از صفر را اعداد طبیعی گویند.
N = {1, 2, 3, 4, 5,…..}
اعداد صحیح :
مجموعه اعداد مثبت و منفی صحیح را اعداد صحیح نامند.
Z = {…,-3,-2,-1, 0, 1, 2, 3,…}
اعداد اعشاری : 5/71 و 14/3
اعداد اول
اعداد اول : هر عدد طبیعی بزرگتر از 1 که غیر از خودش و 1 مقسوم علیه دیگری نداشته باشد، عدد اول نامیده می شود.
P = {2,3,5,7,11,13,17,19,23,29,31,37,41,43,……}
اعداد مثبت : کلیه اعداد بزرگتر از صفر اعداد مثبت هستند. 5 و 1
اعداد منفی : کلیه اعداد کوچکتر از صفر اعداد منفی هستند. -6 , -3
اعداد کسری : ، ، ،
هر عدد به صورت که در آن a , b اعداد صحیح می باشند و b ≠0 باشد یک کسر نامیده می شود.
اعداد گویا : هر عددی که بتوان به صورت کسر نوشت یک عدد گویا است.
اعداد گویا را با Q نمایش می دهند.
هر عدد صحیح یک عدد گویاست.
عدد گنگ : عددی که قابل تبدیل به نسبت دو عدد درست نباشد، عدد گنگ (اصم) است.
اعداد گنگ را با (Q`) نمایش می دهند.
مجموعه اعداد گویا و گنگ را اعداد حقیقی گویند و با (R) نمایش می دهند.
متر
متر = صد سانتیمتر یک متر است.
کیلومتر = 1000 متر یک کیلومتر است.
سانتی متر = 10 میلیمتر یک سانتی متر است.
میلیمتر = یک میلیمتر برابر 1000 میکرون است.
دسی متر = 10 سانتیمتر یک دسی متر است.
دکامتر = 10 متر
هکتو متر = 100 متر
ذرع = 104 سانتیمتر
متر مربع برابر است با مربعی که هر ضلع آن 1 متر باشد.
1 اینچ = 54/2 سانتیمتر
1 فوت = 5/30 سانتی متر
1 یارد = 44/91 سانتی متر
1 مایل = 609/1 کیلومتر
هکتار = 10.000 متر مربع
جریب = 4050 متر مربع
1 کیلومتر مربع = 100 هکتار
لیتر
واحد اندازه گیری مایعات لیتر است.
لیتر = یک لیتر برابر است با گنجایش مکعبی تو خالی که هر بعد آن 10 سانتیمتر باشد.
یک لیتر آب تقریبا برابر یک کیلوگرم می باشد.
سانتی متر مکعب = حجم مکعبی که هر یک از ابعاد آن 1 سانتی متر باشد، یک سانتی متر مکعب است.
متر مکعب = یک متر مکعب گنجایش مکعبی تو خالی به ابعاد یک متر است.
1000 لیتر برابر یک متر مکعب است.
سی سی = یک سانتیمتر مکعب برابر یک سی سی است .
یک لیتر = برابر 1000 سی سی است.
اوزان و مقیاس ها
گرم = هزار گرم برابر است با 1 کیلوگرم
کیلوگرم = 1000 گرم
تن = 1000 کیلوگرم
من = 3 کیلوگرم
خروار = 100 من
سیر = 75 گرم
چارک = 750 گرم
قیراط = 9/205 گرم
1 اونس = 35/28 گرم
1 پوند = 592/453 گرم
1 ری = 12 کیلو گرم
1 مثقال = 6875/4 گرم
1 نخود : 1953/0 گرم
1 گندم = 0488/0 گرم
واحدهای شمارش :
انسانها از گذشته تا کنون برای شمارش اشیاء از اصطلاحات زیر استفاده می کنند :
انسان (شتر و درخت خرما) = نفر
کشتی و هواپیما = فروند
پرندگان = عدد
خانه ، مغازه = باب
کتاب = جلد
کاغذ = برگ
دسته های کاغذ و مقوا = بند
پارچه و کالاهای تجاری = عدل
 مانند
مانند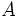 میتوان عددی را نسبت داد.این عدد را با نماد
میتوان عددی را نسبت داد.این عدد را با نماد 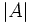 یا
یا 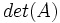 نمایش میدهیم و آن را دترمینان
نمایش میدهیم و آن را دترمینان 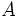 میخوانیم.
میخوانیم. 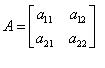
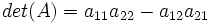
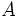 را با
را با 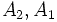 نشان دهیم آنگاه
نشان دهیم آنگاه 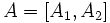 و خواهیم داشت :
و خواهیم داشت :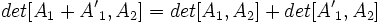
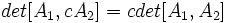
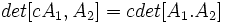
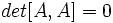
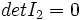
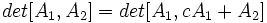
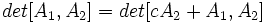
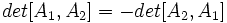
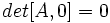
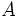 یک ماتریس مربع از مرتبه
یک ماتریس مربع از مرتبه  باشد آنگاه ماتریس حاصل از حذف سطر
باشد آنگاه ماتریس حاصل از حذف سطر 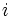 ام و ستون
ام و ستون 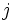 ام که یک ماتریس از مرتبه
ام که یک ماتریس از مرتبه 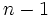 در
در 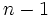 است را با نماد
است را با نماد 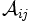 نمایش میدهیم.در اینصورت:
نمایش میدهیم.در اینصورت: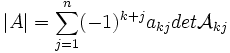
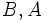 دو ماتریس باشند آنگاه:
دو ماتریس باشند آنگاه: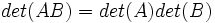
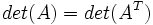
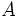 وارون پذیر باشد آنگاه
وارون پذیر باشد آنگاه 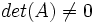
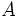 از مرتبه
از مرتبه  مضربی از ستون دیگر آن باشد آنگاه
مضربی از ستون دیگر آن باشد آنگاه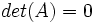
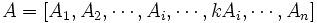
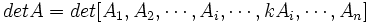
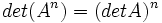
 عمل میکنیم:
عمل میکنیم: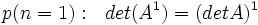
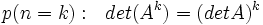
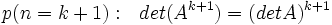






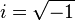 ) بسط داد. اعدادی به فرم a + bi که در آن a و b هر دو عدد حقیقی هستند را اعداد مختلط مینامند.
) بسط داد. اعدادی به فرم a + bi که در آن a و b هر دو عدد حقیقی هستند را اعداد مختلط مینامند.